Ma trận suy biến là một khái niệm nền tảng trong đại số tuyến tính, ảnh hưởng lớn đến việc giải phương trình, thiết kế mô hình và phân tích dữ liệu. Việc nhận biết và xử lý ma trận suy biến không chỉ là kỹ thuật toán học mà còn là kỹ năng thực tế trong kỹ thuật, khoa học máy tính và tài chính.. Theo dõi nội dung được Wikihay chia sẻ để biết thêm thông tin chi tiết về ma trận suy biến là gì?
Khái niệm ma trận suy biến là gì?
Ma trận suy biến là ma trận không khả nghịch, tức là không tồn tại ma trận nghịch đảo của nó. Cụ thể hơn, một ma trận vuông 𝐴 ∈ 𝑅^ (𝑛 × 𝑛) được gọi là suy biến nếu: det(A)=0

Ma trận suy biến là gì?
Điều này đồng nghĩa với việc:
- Không thể tìm được ma trận 𝐴 − 1 A −1 sao cho 𝐴 ⋅ 𝐴 − 1 = 𝐼 A⋅A −1 =I (với 𝐼 I là ma trận đơn vị).
- Ma trận không khả nghịch, không thể dùng để giải trực tiếp hệ phương trình tuyến tính bằng phương pháp nhân ma trận nghịch đảo.
Dấu hiệu nhận biết ma trận suy biến
Ngoài việc kiểm tra định thức bằng tay có nhiều cách nhận biết một ma trận là suy biến:
- Định thức bằng 0: Như đã nói, nếu det ( 𝐴 ) = 0 det(A)=0, ma trận là suy biến.
- Các hàng hoặc cột tuyến tính phụ thuộc: Nếu một hàng là tổ hợp tuyến tính của các hàng khác thì ma trận là suy biến
- Hạng của ma trận nhỏ hơn kích thước: Nếu một ma trận vuông n x n có rank<n thì nó là ma trận suy biến
- Hệ phương trình Ax=b không có nghiệm duy nhất. Trong nhiều trường hợp, một ma trận suy biến không thể dùng để giải hệ có nghiệm duy nhất
So sánh ma trận suy biến và không suy biến là gì?
Đối với ma trận suy biến
- Không có ma trận nghịch đảo: Đây là tính chất quan trọng nhất và là lý do chính mà chúng ta gọi nó là “không khả nghịch”. Nếu det(A)=0, không tồn tại ma trận A −1 sao cho A⋅A −1 =A −1 ⋅A=I (ma trận đơn vị).
- Hệ phương trình tuyến tính:
- Hệ phương trình tuyến tính Ax=b có thể không có nghiệm hoặc có vô số nghiệm. Nó sẽ không bao giờ có nghiệm duy nhất.
- Hệ phương trình tuyến tính thuần nhất Ax=0 (với 0 là vectơ không) luôn có vô số nghiệm không tầm thường (tức là có nghiệm khác x=0).
- Hạng của ma trận: Hạng (rank) của một ma trận suy biến luôn nhỏ hơn cấp của nó (rank(A)<n, với n là cấp của ma trận vuông A).
- Vectơ riêng và giá trị riêng: Ma trận suy biến luôn có ít nhất một giá trị riêng bằng 0.
- Sự phụ thuộc tuyến tính: Các hàng (hoặc các cột) của ma trận suy biến là phụ thuộc tuyến tính với nhau.
- Phép biến đổi không gian: Khi ma trận A được xem như một phép biến đổi tuyến tính, nếu A là ma trận suy biến, nó sẽ thu gọn không gian
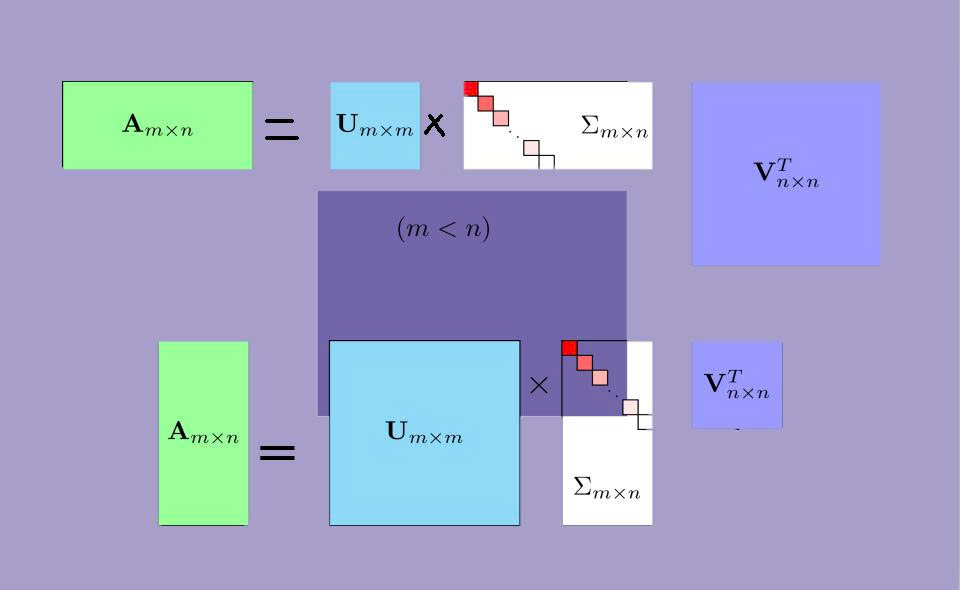
So sánh ma trận suy biến và không suy biến
Đối với ma trận không suy biến
- Có ma trận nghịch đảo: Đây là tính chất cốt lõi. Nếu det(A) =0, thì luôn tồn tại duy nhất một ma trận nghịch đảo A −1 sao cho A⋅A −1 =A −1 ⋅A=I.
- Hệ phương trình tuyến tính:
- Hệ phương trình tuyến tính Ax=b (với b là vectơ bất kỳ) luôn có duy nhất một nghiệm. Nghiệm này có thể tìm được bằng công thức x=A −1 b.
- Hệ phương trình tuyến tính thuần nhất Ax=0 chỉ có nghiệm tầm thường duy nhất là x=0.
- Hạng của ma trận: Hạng của một ma trận không suy biến luôn bằng cấp của nó
- Vectơ riêng và giá trị riêng: Ma trận không suy biến không có giá trị riêng nào bằng 0.
- Sự độc lập tuyến tính: Các hàng (và các cột) của ma trận không suy biến là độc lập tuyến tính với nhau.
- Phép biến đổi không gian: Khi ma trận A được xem như một phép biến đổi tuyến tính. Nếu A là ma trận không suy biến, nó sẽ biến đổi không gian mà không làm giảm chiều
Ứng dụng của ma trận này trong thực tế
Dù không dùng để giải hệ phương trình duy nhất, ma trận này vẫn đóng vai trò nhất định trong các lĩnh vực:
Phân tích dữ liệu và giảm chiều
- Trong học máy và xử lý tín hiệu, một ma trận dữ liệu trở nên suy biến nếu nhiều thuộc tính tương quan với nhau. Từ đó người ta dùng phương pháp như phân tích thành phần chính (PCA) để loại bỏ chiều thừa
Phát hiện đa cộng tuyến trong hồi quy tuyến tính
- Ma trận suy biến thường là dấu hiệu của đa cộng tuyến, tức là các biến đầu vào trong mô hình hồi quy có quan hệ tuyến tính với nhau. Điều này khiến cho việc ước lượng hồi quy kém chính xác.
Xác định điều kiện bài toán
- Trong tính toán số, kiểm tra giúp xác định một bài toán có ổn định hay không. Nếu ma trận gần suy biến thuật toán số có thể cho kết quả sai lệch lớn.
Cách xử lý ma trận suy biến
Sử dụng giải pháp xấp xỉ
- Thay vì tìm nghịch đảo, có thể dùng các phương pháp:
- Nghiệm bình phương tối tiểu (least squares)
- Phân rã ma trận (LU, QR hoặc SVD)
Thêm điều kiện ràng buộc hoặc giảm chiều dữ liệu
- Trong hồi quy, có thể loại bỏ biến dư thừa để tránh ma trận suy biến
- Trong xử lý tín hiệu, PCA hoặc phân rã SVD thường được dùng
Một số lưu ý bạn cần biết
- Không phải mọi ma trận đều có nghịch đảo. Chỉ ma trận vuông và không suy biến mới có.
- Kiểm tra định thức là cách nhanh nhất để xác định tính suy biến.
- Trong lập trình (Python/NumPy, MATLAB…), nếu bạn cố dùng np.linalg.inv() cho một ma trận suy biến, sẽ bị lỗi.
Tổng kết
Thông tin về khái niệm của ma trận suy biến là gì được Wikihay tổng hợp và chia sẻ đến bạn. Hi vọng qua nội dung được chia sẻ sẽ giúp ích đến bạn. Đừng bỏ qua những bài viết khác được chia sẻ từ hệ thống chúng tôi để biết được nhiều thông tin hữu ích khác.











Để lại một bình luận